Tactile Maps from Gaussian Process Implicit Surface
I. Gaussian Process
0. Basic Assumption
☝🏻Gaussian distribution is the key assumption here! Take a Gaussian distribution adding it up with another Gaussian distribution gives you a Gaussian distribution, multiplying, marginalizing, normalizing all gives you a ?Gaussian distribution, and most importantly conditioning also gives you a Gaussian distribution:
\[\left \{ a, b \right \} \sim \aleph \to \left \{ P(a, b), P(a \mid b), P(a)=\int\limits_{b}^{}p(a,b)db \right \} \sim \aleph(\mu, \varepsilon)\]
1. Modeling on $\mathbf{w}$
Given a linear regression, with known dataset of \(D=\left \{ (\mathbf{x}_1, \mathbf{y}_1), ..., (\mathbf{x}_n, \mathbf{y}_n) \right \}\) , we intend to learn the parameter $\mathbf{w}$ and built the prediction model of $f(\mathbf{x})=\mathbf{w}^T\mathbf{x}+\varepsilon$ , that $\varepsilon \sim \aleph(0, \sigma^2I)$ represents the prediction noise and is in Gaussian distribution.
There’re two general different approaches to learn the $\mathbf{w}$:
Maximize Likelihood Estimation (MLE):
\[\begin{equation}P(D \mid \mathbf{w}) = \prod_{i=1}^{n}p(\mathbf{y}_i \mid \mathbf{x}_i, \mathbf{w}) \end{equation}\]Given the parameter \(\mathbf{w}\), how likely each of particular \(\mathbf{x}_i\) gives a prediction on right label \(\mathbf{y}_i\). \(\mathbf{w}\) is the best interpretation on data $D$. Moreover, \(p(\mathbf{y}_i \mid \mathbf{x}_i, \mathbf{w}) \sim \aleph(\mathbf{w}^T\mathbf{x}_i, \sigma^2I)\) coming from the \(f(\mathbf{x})=\mathbf{w}^T\mathbf{x}+\varepsilon\) , thus making the \(P(D \mid \mathbf{w})\) also a Gaussian.
Maximize A Posteriori Estimation (MAP):
\[\begin{equation}P(\mathbf{w} \mid D)\propto \frac{P(D \mid \mathbf{w})P(\mathbf{w})}{Z} \end{equation}\]Given the dataset $D$, what is the most likely set of parameters $\mathbf{w}$. This probability could be express as above in Bayesian Rules, where $P(D \mid \mathbf{w})$ is a Gaussian distribution according to eq.1.
The general objective here is to fit the $D$ by a set of parameter $\mathbf{w}$ to make a determined final prediction $\mathbf{y}$, as $D \to \mathbf{w} \to \mathbf{y}=\mathbf{w}^T\mathbf{x}$. This is a an overview when we trying to model the probability of $\mathbf{w}$ here in linear regression to make final prediction on test point. This leads to our main target here today of Gaussian Process which on the contrary trying to model the prediction at test point from the start, instead of modeling the $\mathbf{w}$.
\[P(\mathbf{y}_* \mid \mathbf{x}_*, D)\]where, \(\mathbf{y}_*\) and \(\mathbf{x}_*\) represent the test point input and corresponding prediction.
2. It is a Gaussian!
We can skip the procedure of modeling parameter $\mathbf{w}$, by marginalize out the model, as follows:
\[\begin{equation}P(\mathbf{y}_* \mid \mathbf{x}_*, D)=\int\limits_{\mathbf{w}}^{}p(\mathbf{y}_* \mid \mathbf{x}_*, \mathbf{w})p(\mathbf{w} \mid D)d\mathbf{w} \end{equation}\]In order to make a prediction, we have to have a model \(p(\mathbf{y}_* \mid \mathbf{x}_*, \mathbf{w})\) and we know what the probability of \(\mathbf{w}\) is here \(p(\mathbf{w} \mid D)\) and we can marginalize it by integrate out all possible values.
☝🏻We can always add another variable and then marginalize it out by integrating out all possible values, it doesn’t mean anything:
\[P(\mathbf{y}_* \mid \mathbf{x}_*, D)=\int\limits_{\mathbf{w}}^{}p(\mathbf{y}_* \mid \mathbf{x}_*, D, \mathbf{w})d\mathbf{w}\]And then transform the above equation into eq.3, prediction $\mathbf{y}_*$ depends on a imaginary set of parameter $\mathbf{w}$ and $\mathbf{w}$ depends on the $D$.
Take equation (1) and (2) into (3), we already know \(p(\mathbf{y}_* \mid \mathbf{x}_*, \mathbf{w}) \sim \aleph(\mathbf{w}^T\mathbf{x}_*, \sigma^2I)\) is a Gaussian distribution, \(p(\mathbf{w} \mid D)\) is also a Gaussian distribution after normalizing from two other Gaussians in eq. 2. BTW, as the basic assumption here, $P(\mathbf{w})$ is also a Gaussian otherwise all the calculation would fall apart. This is a easy and reasonable assumption. In this way, we finally skip the modeling on parameters, and build a direct modeling on prediction of test point. IT IS A GAUSSIAN!!! We just need to know the expectation and variance of this new Gaussian \(P(\mathbf{y}_* \mid \mathbf{x}_*, D)\), how it looks like.
\[P(\mathbf{y}_* \mid \mathbf{x}_*, D) \sim \aleph(\mu_*, \Sigma_*) \\P((\mathbf{y}_1, ..., \mathbf{y}_n)^T \mid (\mathbf{x}_1,...,\mathbf{x}_n))\sim \aleph(\mu, \Sigma)\]Basically it builds a direct mapping from training data to the test point data based on its probability distribution. The $\Sigma$, as the covariance matrix between training data, represents the correlation from it. The main task here is to update the $\mu$ and $\Sigma$ every time there’s a new training data input and calculate the \(\mu_*\) and \(\Sigma_*\) at the test point. So as you can imagined, it would cost space to maintain this increasingly big covariance matrix from continuous inputting training data, yet it benefit from a prediction with uncertainty (it is not just a determined prediction but with expectation and variance)
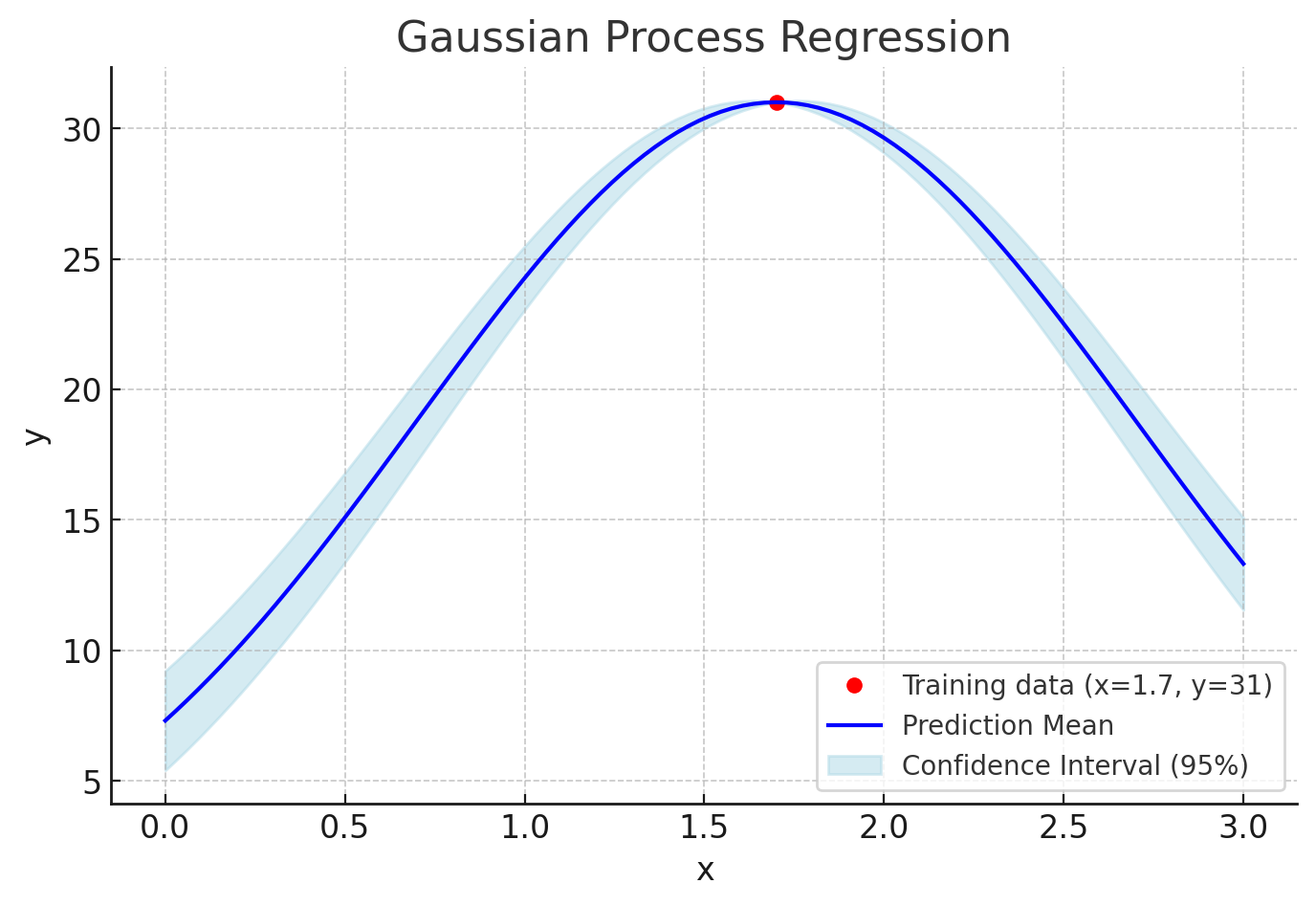
Give an example here. If we already knew a input $x=1.7$ gives a output $y = 31$, then we probably could give reasonable speculation that the input $x=1.8$ correspond to a out $y$ not far from $31$, let’s say $33$, but the input $x=12.2$’s correspondent output would be hard to presume since it is too far from the last training point. Thus we can say, the training data of $x=1.7$ significantly correlates to our test point $x=1.8$ which is near the $1.7$.
The mean value of $\mu$ here is not that much important comparing with the covariance matrix. Most of the time, we just set the default mean to $0$ and it could start to update the Gaussian distribution from a bias of $0$. Let’s say, if we want to set the default mean $\mu$ to 30, what would happened? This was added directly to the Gaussian Process’ prediction and led to the model starting with an initial bias of 30 across the whole input space.
3. Update the Gaussian
OK, we have prove every details of the assumption here: given training data $D$ and the input value \(\mathbf{x}_*\), the probability distribution of the test point prediction \(\mathbf{y}_*\) is a Gaussian distribution. Now the left issue is how to calculate this distribution.
We need a positive semi-definite matrix represents the covariance matrix $\varepsilon$, which is a KERNEL $K$! And a evaluation function $k(\cdot)$ to formulate the matrix by evaluating the correlation from the input training data to itself and and also unknown test point. I will skips several details here and go directly to the key equations we would actually need to calculate the results.
The joint distribution of function values from test point and training set can be written as:
\[\begin{pmatrix}f(X) \\f(X_*)\end{pmatrix}\sim \mathcal{N} \left(\begin{pmatrix}\mu(X) \\\mu(X_*)\end{pmatrix},\begin{pmatrix}K(X, X) & K(X, X_*) \\K(X_*, X) & K(X_*, X_*)\end{pmatrix}\right)\]$K(X, X)$ is the covariance matrix of inner training data where each entry is $K_{ij}=k(\mathbf{x}_i, \mathbf{x}_j)$.
To calculate the conditional distribution of test point \(P(\mathbf{y}_* \mid \mathbf{x}_*, D) \sim \aleph(\mu_*, \Sigma_*)\):
$\mu_*$ the mean prediction is given by:
\[\mu_* = K(X_*, X) \left[ K(X, X) + \sigma_n^2 I \right]^{-1} y\]$\Sigma_*$ the covariance of the prediction is given by:
\[\Sigma_* = K(X_*, X_*) - K(X_*, X) \left[ K(X, X) + \sigma_n^2 I \right]^{-1} K(X, X_*)\]II. Implicit Surface
☝🏻An implicit surface is a type of surface defined by an equation rather than by a set of points (explicit surfaces). Specifically, it’s defined by an equation $f(x)=0$ where $f$ is a scalar function, and $x$ represents points in some multidimensional space.
We have already used it in our previous whisker characterized deflection profile extraction process, by use the custom fixed $z$ measurement value as the scalar output, to represent a implicit curve in the 2-dim space. I just need to familiarize myself with some context here before I dive into the Gaussian Process Implicit Surface (GPIS)
Many applications in computer vision and computer graphics require the definition of curves and surfaces. Implicit surfaces are a popular choice for this because they are smooth, can be appropriately constrained by known geometry, and require no special treatment for topology changes. Given a scalar function $f : \mathbb{R}^d \to \mathbb{R}$ one can define a manifold $S$ of dimension $d − 1$ wherever $f(x)$ passes through a certain value (e.g., $0$)
\[S_0 \triangleq \{ x \in \mathbb{R}^d \mid f(x) = 0 \}.\]