Adopt an Gradient Descent Method to Find the Contact Position on Tip

👉🏻 This is a back-up plan if the dynamic error could not be compensate by the fading memory filter and quasistatic hypothesis in a fast sampling rate in a solution based on sequential state estimate. The major limitation of this solution is the contact can only happened on the tip of whisker.

---

General Principle

The start point around basement, total length of the shaft body, the instantaneous deflection curve profile can be acquired from finite element analysis on suspension device, predefined measurement and fitted measurement model based on 5-order bivariate polynomial respectively. Based on that, we shall let the estimate flow from start point alone the certain curve profile in a predefined distance, and the end point is just the tip position of this shaft on current deflection iteration. And of course, this asks the contact to be restricted on tip. We call that a tip-tap contact mode.

Major Prerequisite

• Start point $P_{s}=(x, y)$.

Theoretically, the start point or to say, the root of whisker device basement is not actually fixed. The deflection along the whisker will certainly cause a movement on magnet and the center of suspension device. That motion can be modeled based on finite element analysis (FEA) on the mechanical structure of device. But for now, it is too much expensive to conduct and even though an error on estimate yet not that much significant. Therefore, we manually set the start point at $(50, 196)$, it is cheap and enough accurate. Or we can find a predefined root height $y$ and calculate the respective start $x$ from measurement model with current constant $z$. But It’s not say it really helps on a better accuracy since the measurement model is still not accurate especially around the area of root and the a fixed root height is based on a hypothesis that the device center’s movement was composed of translation. The rotation can’t be ignored.

• Total length $L$.

From magnet to whisker root (3.5 $mm$, the measurement is on our built 3D model) then to whisker tip (75.5 $mm$), a total length of 79 $mm$.

• Curve profile $z=f(x, y)$.

It is originally built for the state estimate solution. The motorized stage move in a grid-like form on 2D plane with certain step distance along x- and y-axis, to contact the whisker on different position and collect the corresponding magnetic vector, and build a fitted polynomial $f(\cdot)$. Under every instantaneous moment, the $z$ is a constant value of current magnetic measurement, which deduce it to a bivariate function on $x$ and $y$ as a curve profile.

Gradient Descent

Based on the content we discussed above, it has been able to obtain all the major values for the calculation. The only thing left is to find an method letting the estimate sweep from the root to the tip. Here we conduct a gradient descent like method to achieve that. Tow major sweep direction were defined here.

Loss direction

We want the trajectory to be as close as possible to the origin curve profile. Therefore, a gradient of the squared error loss function on distance was first built.

def loss_gradient_z(x, y, target_z):
    """ Gradient of the squared error loss function. """ 
    
    error = z_polyval(x, y, coeff) - target_z
    grad_z = gradient_z(x, y)
    return 2 * error * grad_z

z_polyval function produce a new measurement on current position and subtract a target measurement target_z where it is a constant value on current curve profile.

Tangent direction

The minimum loss direction will lead the sweep onto the current curve and stop to change, since it has been the most close point to the profile. Therefore, we have to motivate the movement of sweep nevertheless to a random direction. And a tangent direction would be reasonable.

def gradient_z(x, y):
    """ Gradient of the function f(x, y). """ 
    
    dzdx = 8.44884428670741e-7*x**2*y**3 - 0.00123376612131287*x**2*y**2 + 0.302732827643646*x**2*y - 20.4489160738201*x**2 + 0.000132670716289769*x*y**3 - 0.0123208056132376*x*y**2 - 4.8753886388656*x*y + 553.746193251521*x - 0.00368917790303178*y**3 + 1.08592170689341*y**2 - 79.4652582182248*y + 14.7548927606983
    dzdy = 8.44884428670741e-7*x**3*y**2 - 0.000822510747541916*x**3*y + 0.100910942547882*x**3 + 0.000199006074434653*x**2*y**2 - 0.0123208056132376*x**2*y - 2.4376943194328*x**2 - 0.0110675337090953*x*y**2 + 2.17184341378682*x*y - 79.4652582182248*x + 0.0868663906400725*y**2 - 17.0871247298984*y + 684.458789414091
    return np.array([dzdx, dzdy], dtype=np.float64)

The gradient_z calculate the tangent direction on every possible position in 2D-plane. The predefined parameter configuration is transformed from the coefficient matrix of the fitted polynomial model.

Step along the profile

Finally we can drive the sweep with a configurable step_size and gradient combining the tangent movement and minimum loss direction, tangent_direction[:] - loss_direction[:]. The delta_dis is for calculate the accumulate moving distance and compare with the predefined $L$, exit the loop after passing it.

dx = step_size * (tangent_direction[0] - loss_direction[0])
dy = step_size * (tangent_direction[1] - loss_direction[1])
delta_dis += np.sqrt(dx**2 + dy**2)

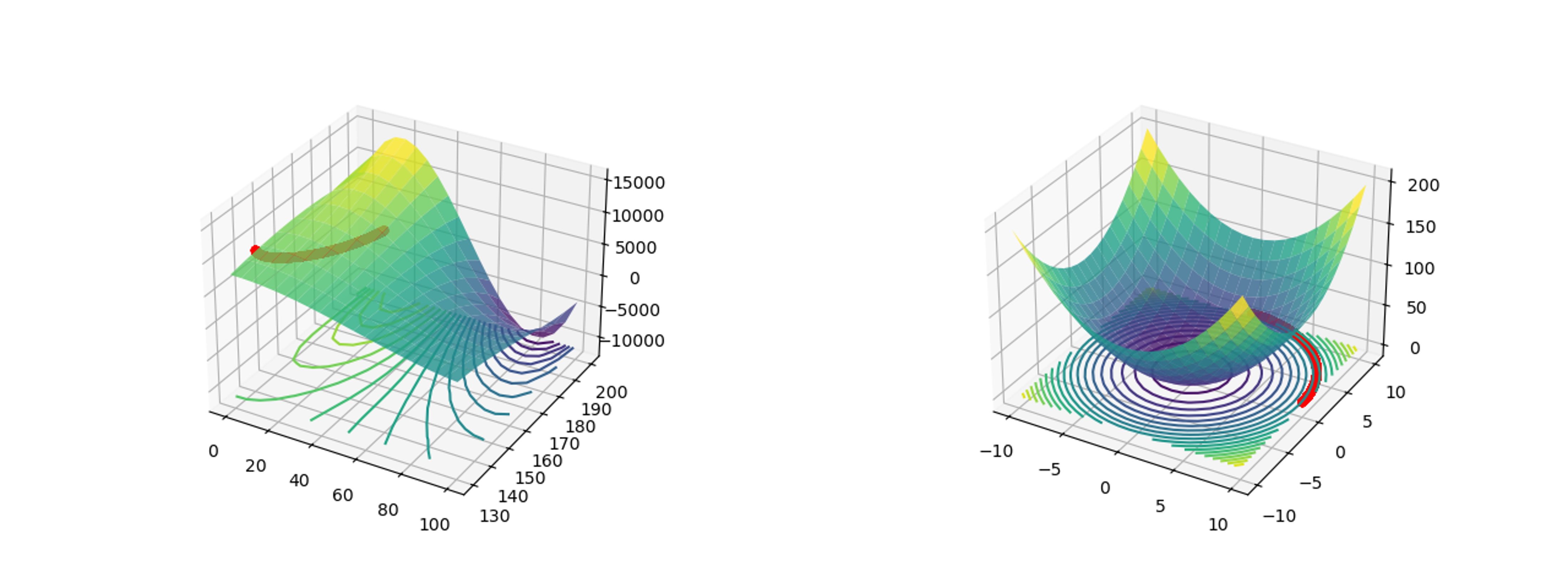Sweep along a circle surface & a certain deflection profile of whisker

Some other issues

Numerical stability issues

There are some issues we may encounter in the implementation.

⚠️ Runtime Warning: overflow encountered in scalar power

happens when the calculation exceeds the maximum value that can be represented by the numpy data type (usually float64). This often occurs during polynomial evaluations where coefficients are multiplied by large powers of variables.

⚠️ Runtime Warning: overflow encountered in multiply

suggests that an operation attempted to multiply by a NaN (not a number) or infinite value.

⚠️ Runtime Warning: invalid value encountered in divide

is often due to attempting to divide by zero, which happens if the norm of the vector tangent_direction is zero.

Basically, it’s just because the decimal is too large and float exceeds its maximum. We already use a float64 to avoid that yet doesn’t work. At the end we solve it by reduce the step size. But I suppose we could still encounter a potential numerical stability issues if we want to enlarge our polynomial model by order in the future.

Sympy to solve the equation

⚠️ Type Error: loop of ufunc does not support argument 0 of type Float which has no callable sqrt method

The TypeError: loop of ufunc does not support argument 0 of type Float which has no callable sqrt method error typically occurs when using NumPy’s functions, like np.sqrt, with data types that NumPy does not recognize or cannot handle. In this case, the error message indicates that you’re trying to use a Float **type with NumPy, which is likely a sympy.Float object rather than a native Python float or a NumPy float64.

We apply a Sympy to transform the predefined coefficient matrix and instantaneous measurement into bivariate function about $x$ and $y$, and calculate its partial derivative. Thus we shall turn it into numpy format before we conduct the calculation.